Jwanna Story

코드는 제일 하단에 위치해있습니다.

해당 문제 : https://www.acmicpc.net/problem/1074

1. 접근 방법 

Z모양 순서로 2차원 배열을 탐색하는 문제이다.

2^N × 2^N 배열을 4구역으로 나누어 탐색하므로 4개의 사분면으로 구분할 수 있고,

분할 정복 문제이므로 재귀를 이용하여 문제를 풀 수 있다. ( 물론 반복문으로도 가능하다. )

여기까지 보고 뭔가 떠올랐다면 스스로 생각을 해서 풀어보는 것도 좋겠다.

2. 풀이 설명 

지금부터 배열의 4구역을 0, 1, 2, 3으로 나눌 것이다.

( 재귀로 풀 것이므로 Top-Down 방식의 풀이를 설명한다. )

만약 2^3 × 2^3 배열에서 4구역을 나눈다면 아래 표와 같이 나눌 수 있을 것이다.

또한, 각 구역의 (0, 0) 좌표에 해당하는 값들은 규칙성이 있다.

위 배열은 2^3 × 2^3 배열이고, 1구역의 (0, 0) 좌표에 해당하는 값은 16이다.

16은 4^2로 나타낼 수 있고, 이는 2^N × 2^N 배열에서 1구역의 (0, 0)에 해당하는 값은 4^(N-1)이라고 할 수 있다.

이런식으로 각 구역의 (0, 0) 좌표를 살펴보면, 2구역은 1구역의 2배, 3구역은 3배인 것을 볼 수 있다.

따라서, 각 구역의 (0, 0) 좌표 값은 4^(N-1) * 구역번호로 나타낼 수 있다.

이제 입력받은 행(Row)과 열(Column)에 따라 해당 좌표가 어느 사분면에 위치해 있는지 확인해야한다.

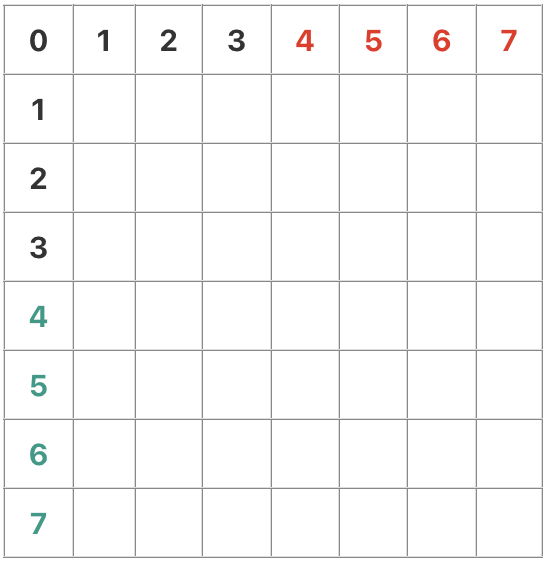
위의 2^3 × 2^3 배열에서 (0~3)과 (4~7)로 구역이 나뉘고 있고, 

Row나, Column 값이 4이상 인가? 를 판별하면 각 구역을 구분할 수 있다.

여기서 4는 2^2으로 나타낼 수 있고, 2^N × 2^N 배열에서 각 구역을 구분하는 기준은 2^(N-1)보다 Row나 Column 값이 큰 가? 로 나타낼 수 있다.

이제 구분 기준도, 값을 추가하는 방식도 정했으니 재귀 호출을하면 된다.

1. R, C의 위치를 확인해서

2. 구역을 나눈 뒤

3. 해당 구역의 (0, 0) 값을 결과 변수에 저장하고

4. x, y 좌표를 다시 (0, 0) 부터 시작하게끔 설정해주고

5. …

6. 구역이 없어지면 종료

이런 식으로 재귀를 해야 한다.

📌 작성한 코드

import java.io.*;
import java.util.*;

public class Main_1074 {
    public static void main(String[] args) throws IOException {
        BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(input.readLine());
        int n = Integer.parseInt(st.nextToken());
        int y = Integer.parseInt(st.nextToken());
        int x = Integer.parseInt(st.nextToken());

        // 결과값을 저장할 변수
        int result = 0;

        // 재귀
        System.out.println(z(n, x, y, result));
    }

    public static int z(int n, int x, int y, int result) {
        // n 이 1이 되면 마지막 결과를 구해야한다. (좌표 값에 따라) 0, 1, 2, 3 중에서 값이 있다.
        // 사분면으로 나누었을때 해당 사분면의 (0,0) 값은 [4^(n-1) * (0~3)]이다.
        // 재귀를 돌 때 해당 값을 result 에 추가하고 n을 1씩 감소시키면서 사분면을 계속 탐색한다.
        // 어떤 사분면에 위치하는지에 따라 좌표값도 계속 수정해준다.
        // 0 -> [x-2^(n-1)]

        // n == 0 일 때 ( 재귀 종료 조건 )
        if (n == 0) return result;

        // 해당 (x, y) 좌표의 사분면 구하고, (x, y) 좌표 수정하기
        // 구역을 구분하는 기준 half = 2^(n-1)
        int half = (int) Math.pow(2, n-1);
        int quadrant;

        if(x >= half && y >= half) {
            quadrant = 3;
            x -= half;
            y -= half;
        }
        else if(x < half && y >= half) {
            quadrant = 2;
            y -= half;
        }
        else if(x >= half && y < half) {
            quadrant = 1;
            x -= half;
        }
        else quadrant = 0;

        // 사분면에 따라 result 값 추가하기 [ 4^(n-1) * (0~3) ]
        int initNum = (int) Math.pow(4, n-1);
        result += (initNum * quadrant);

        // 재귀 호출 (n을 1씩 감소시키면서)
        return z(--n, x, y, result);
    }
}

RESULT